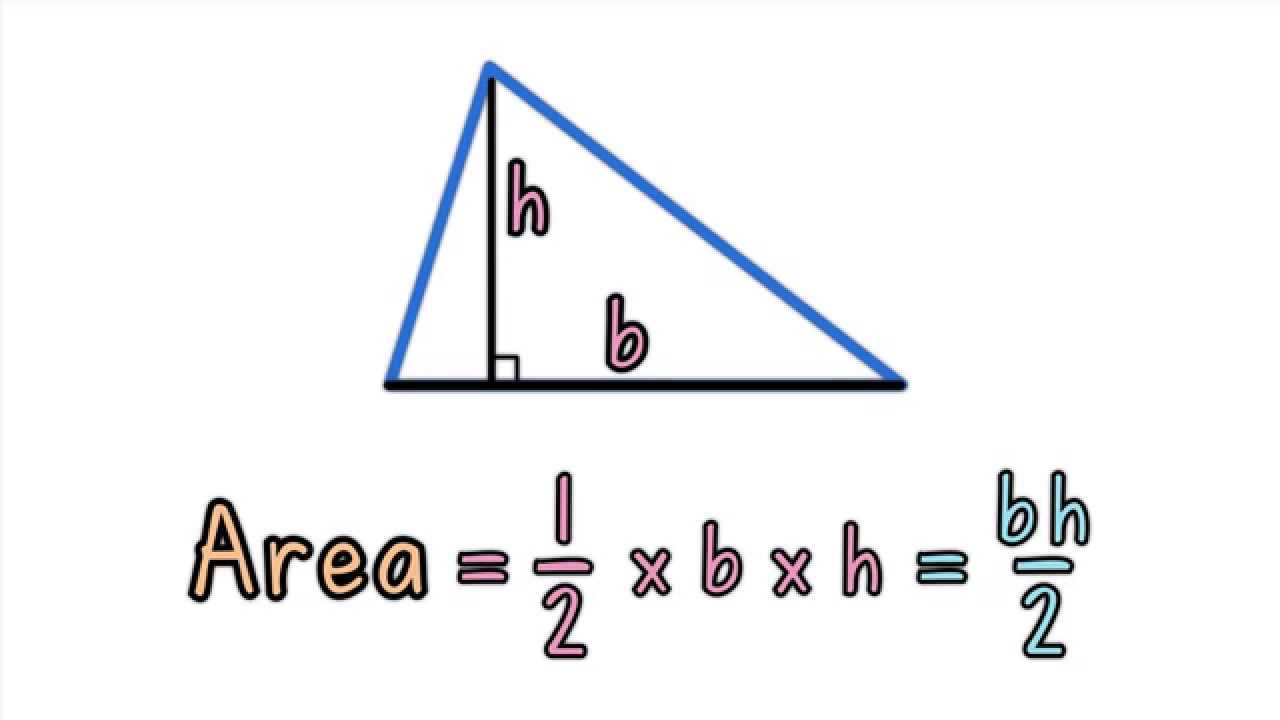How To Find Height With Volume And Base Area

Volume is the quantification of the three-dimensional space a substance occupies. The SI unit for volume is the cubic meter, or m3. Volumes of many shapes can be calculated by using well-defined formulas.

In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume. The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary. Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method. Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. This calculator computes volumes for some of the most common simple shapes. We can also define the cone as a pyramid with a circular cross-section, unlike a pyramid that has a triangular cross-section.

Let us study the cone height formula using solved examples at the end of the page. The cone height formula helps in calculating the distance from the vertex of the cone to the cone's base. The height of the cone can be calculated using either the volume of cube and radius or with slant height and radius of the cone. In geometry, a cylinder is a three-dimensional shape with a circular base, a circular top and straight sides. It is the solid figure that you get when you rotate a rectangle about one of its sides.

In most cases when we talk about the volume of a cylinder, we are talking about how much liquid it can hold. A pyramid consists of three or four triangular lateral surfaces and a three or four sided surface, respectively, at its base. When we calculate the surface area of the pyramid below we take the sum of the areas of the 4 triangles area and the base square. The height of a triangle within a pyramid is called the slant height. The radius of the base is 4[/latex] centimeters and the height is 13[/latex] centimeters.

Assume the can is shaped exactly like a cylinder. Find the height of a cylinder with a volume of 32 cubic centimeters, which has a base circumference of 3 centimeters. Purpose of useWhat is the volume of the square pyramid, given the base edge and slant height.

Round your answer to the nearest tenth, not using any units of measure in your answers. Thus, to calculate the height, divide the volume of a prism by its base area. Suppose that the volume of the prism is 600 cubic units and its base area is 60 square units. Then, dividing 600 by 60 results in 10.

Each crate is in the shape of a rectangular solid. Its dimensions are the length, width, and height. The rectangular solid shown in the image below has length 4[/latex] units, width 2[/latex] units, and height 3[/latex] units. Can you tell how many cubic units there are altogether? Find the height of a cylinder with volume 25 cubic centimeters which has a base radius of 2 centimeters.

In this example you need to calculate the volume of a very long, thin cylinder, that forms the inside of the pipe. The area of one end can be calculated using the formula for the area of a circle πr2. The diameter is 2cm, so the radius is 1cm.

The area is therefore π × 12, which is 3.14cm2. If you know how to multiply you can find the volume of a cube or box. We learned earlier that the surface area of a flat rectangle was the length times the width, but that was just a flat two-dimensional object. The following table gives the volume formulas for solid shapes or three-dimensional shapes.

How To Find Height Of Cone With Volume And Base Area Scroll down the page if you need more explanations about the volume formulas, examples on how to use the formulas and worksheets. It turns out that the volume formula works just the same for these. You must however use the perpendicular height in the formula. This is the vertical line to left in the figure above. To illustrate this, check 'Freeze height'. As you drag the top of the cylinder left and right, watch the volume calculation and note that the volume never changes.

A prism is a solid figure that has two parallel congruent sides that are called bases that are connected by the lateral faces that are parallelograms. There are both rectangular and triangular prisms. If you have ever seen a can of soda, you know what a cylinder looks like.

A cylinder is a solid figure with two parallel circles of the same size at the top and bottom. The top and bottom of a cylinder are called the bases. The height h[/latex] of a cylinder is the distance between the two bases. For all the cylinders we will work with here, the sides and the height, h[/latex] , will be perpendicular to the bases. We see that finding the height of a cylinder, given its volume and the radius of its circular base, is fairly easy. To find the volume of a rectangular prism, multiply the length, width, and height.

The unit for measuring the volume of a rectangular prism is cubic units, i.e., cm3, mm3, in3, m3, etc. Our height of a cylinder calculator is a handy tool dedicated to the right circular cylinder. This type of cylinders consists of two congruent circles . They lie precisely one above the other, and that's why we call it a right cylinder. On the other hand, if one of the bases is shifted, then a cylinder is oblique.

The term circular is more obvious - bases have the form of circles. You should remember that the word cylinder may correspond to the different shapes , but we usually have in mind the right circular cylinder. There are many applications in real life where the volume calculator is useful. One such instance is in road or pavement construction where slabs of concrete must be built. Generally concrete slabs are rectangular solids, so the rectangular prism calculator can be used. Volume is the amount of total space on the interior of the solid.

Knowing the definition of volume, we can now focus on the formulas for volume of common geometric solids. Using these formulas manually won't be difficult, but for fast, accurate results every time, use the volume calculator. The lateral faces meet at a common vertex.

The height of the pyramid is the perpendicular distance from the base to the vertex. The pyramid is named after the shape of its base. For example a rectangular pyramid or a triangular pyramid. To calculate the area of a triangle, we multiply the base times the height and divide by 2. If you are given the area, follow the steps backwards.

You will multiply by 2 and divide by the given length. Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. Find the perimeter of the triangles having the following sides.

Before we jump into how to find the volume and surface area of a prism, let's go over a few key terms that we will see in our formulas. The first word we need to define is base. The bases of a prism are the two unique sides that the prism is named for. For example, if you have a hexagonal prism, the bases are the two hexagons on either end of the prism.

The surface area S[/latex] of the rectangular solid shown above is 52[/latex] square units. We now have another version of the volume formula for rectangular solids. Let's see how this works with the 4\times 2\times 3[/latex] rectangular solid we started with. A cylinder has height 5[/latex] centimeters and radius 3[/latex] centimeters. Before you can find the height, you need to know the radius of the circular base, and you need to know the volume of the silo. You are able to go inside the empty silo and measure the radius, and you find it to be 8 feet.

Before we can learn how to find the height of a cylinder, we need to quickly review some vocabulary. A cylinder is a three-dimensional object with two equal-sized circular ends. These equal-sized circular ends are called bases.

The height of a cylinder is the distance between the two circular bases. The area of a rectangular prism's base is 25 square inches and its height is 10 inches. Find the volume of this rectangular prism.

Equals the height of the prism.The base of a prism is one of its congruent sides. The base of a triangular prism will be a triangle. Simply enter the dimensions into the calculator to find the volume.

The units for volume will always be cubed, as compared to square units for surface area. Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations. A cylinder is a solid that has two parallel faces which are congruent circles. These faces form the bases of the cylinder.

The height of the cylinder is the perpendicular distance between the two bases. A rectangular solid is also called a rectangular prism or a cuboid. Find the volume and surface area of this regular triangular prism. Find the volume and surface area of this rectangular prism.

For example, the cylinder and cone shown here both have a base with radius 3 feet and a height of 7 feet. It is a three-dimensional, box-like shape that can be represented only in the three-dimensional plane. It has six faces, each of which is rectangular in shape.

Thus a cuboid is formed when six rectangles are stacked up together, forming all three proportions of a cuboid, i.e., length, breadth, and height. Mathepower can calculate the base area, lateral area, surface, height and volume of a cone. Just enter your exercise and it will be solved step-by-step.

The volume of the prism is the area of the base times the height. So to calculate height, divide the volume of a prism by its base area. For this example, the volume of the prism is 500 and its base area is 50. For a rectangular solid with length 14[/latex] cm, height 17[/latex] cm, and width 9[/latex] cm, find the 1. Breaking a rectangular solid into layers makes it easier to visualize the number of cubic units it contains. This 4[/latex] by 2[/latex] by 3[/latex] rectangular solid has 24[/latex] cubic units.

A cheerleading coach is having the squad paint wooden crates with the school colors to stand on at the games. The amount of paint needed to cover the outside of each box is the surface area, a square measure of the total area of all the sides. The amount of space inside the crate is the volume, a cubic measure. Students will find the height when the radius, diameter, or circumference of the base is known.

Just split the solid up into smaller parts until you reach only polyhedrons that you can work with easily. Calculate the volume of a solid rectangular prism whose base area is 18 in2 and height is 4 in. A rectangular prism is a 3-dimensional object with six rectangular faces.

A rectangular prism is also referred to as a cuboid, rectangular hexahedron, right rectangular prism, or a rectangular parallelepiped. The volume of a rectangular prism is the measure of the space the fills it. In this article, you will learn how to find a rectangular prism volume by using the volume of a rectangular prism formula. We will also discuss the volume of a spherical cylinder.

Forza Horizon 5 New Cars Reddit

Turn 10 Studios' ForzaMotorsport is a series of simulation racing games that focuses on track racing events, around a variety of real and fictional tracks. The popular game franchise showcases realistic performance and handling characteristics of many real-life production, modified, and racing cars, and is published by Xbox Game Studios. As Xbox Game Studios' popular racing game Forza Horizon 5speeds toward its Nov. 19, 2021 release date, fans are eager to know which tricked-out cars are the best for certain racing scenarios. For instance, the best street racing cars in the game don't always equate to the fastest cars per se, they also take into account factors such as body weight, handling, braking, acceleration, etc.

The Forza Horizon 5 Dec. 3, 2021 patch update focused primarily on fixing online issues, especially with Horizon Arcade. While it is now considerably easier to complete Horizon Arcade events, even by yourself, other elements of FH5's online portions haven't improved. Players are reporting that Horizon Life is now rarely populated by more than one or two additional players, and Convoys are still plagued with the same problems. We've included a fix for civilian traffic not being present in Horizon Life.

However, we know there is more work to do in this area. These are being worked on and will be addressed in a future update. The Forza Edition of the BMW X 5 in Horizon 5 boasts some of the best performance ratings across the board, making it ideal for street and road races. With perfect 10 acceleration, handling, and launch scores to go with a stellar 9.4 braking, very few cars will be able to keep pace with the X5 M. The best overall electric car in Forza Horizon 5 is the Porsche 918 Spyder. With impressive acceleration and launch and fairly high speed, braking and handling stats, the hybrid supercar is one of the game's fastest S2 Class cars in-game.

We are certainly spoilt for choice with the selection of electric cars to enjoy the spoils and earn victories at the Horizon Festival. In terms of which electric cars are some of the best in-game, we compared picks across all car class types based on speed, acceleration, braking, handling, launch and offroad. Forza Horizon 5 has no shortage of electric cars as one player on Reddit asked the Forza community if the game featured any. Here's what you need to know about the game's best electric cars based on speed, acceleration, braking, handling and more.

Playground Games has delivered their latest masterpiece with Forza Horizon 5, which features the series' most diverse map and largest car list yet. Forza Horizon 5 somehow fulfills its ambitious promises to be the best open-world racer right now, and one of the best racing games in general. In our Forza Horizon 5 review, we concluded that Playground Games has delivered the unchallenged champion of open-world racers, and is the quintessential choice on our list of best Xbox racing games. This remains true, even with the persistent online flaws that afflict the title in the weeks after launch. If you want to learn more about this excellent game and everything it has to offer, be sure to check out our ultimate guide to Forza Horizon 5.

I really do like the game, it's all I've played since it came out. I booted up Destiny yesterday loaded into the Tower and was like "nah I'm going back to Horizon." There's obviously things that need to fixed with the game like the AI. The AI's car abilities is what bothers me the most, I wish it reflected their actual car stats more, it's almost as if every car the AI drives is all 10's no matter what it is. Removing the older models is a shame but the fact that a lot of older classic cars are being removed is quite meh to say the least. The carlist was never gonna be FH4 tier at launch but it's looking to be more lacking than previous games were at the start. I just hope there's more unique cars and more newer Audi's, Volkswagen's, Ford's and so on added down the line.

With unmatched perfect 10 ratings for acceleration, braking, handling, and launching, the Lamborghini Sesto Elemento is an absolute street racing beast. The ultra-expensive high-performance sports car comes with a 5.2L naturally aspirated V10 engine to go with its slight 2200-pound chassis and AWD 6-speed transmission. Forza Horizon 4 released more than three years ago, and dedicated players have built up hundreds and hundreds of hours of playtime. However, with a new Forza game comes a fresh, empty garage to fill up, and that means Horizon 4 players are having to say emotional goodbyes to some of their favourite cars. As shared by a friend of the affected playeron Reddit, the disciplinary action was issued as the player's "first-ever in-game ban" without any prior warnings or bans given.

Though this may seem extreme, photos of the car shared along with the post make it pretty clear why the ban was so dramatic. This directly violates a "Forza" rule that prohibits user-generated content of "certain notorious individuals," as pointed out by a Redditor. It's a good idea to pick a road race on a hard surface to help you set your assists, dead zones, and controls for high-performance road and track cars, for the long haul.

We ran the Emerald Circuit in a Ford GT to find a sweet spot for acceleration and traction. Again, some cars are so powerful that you will need traction control. But use it only on the fastest ones in your fleet, as the hit to their acceleration won't be as profound as it is on slower cars. If you aren't knowledgeable about actually tuning cars go to Find Tuning Setups. Here you will see community-created parts-and-tuning packages, with a histogram showing the areas in which they will improve your car's performance.

The Find Tuning Setups panel, and the ability to purchase and apply their parts, is also available before any race from the event's menu. Leaning on others' creations is a good way to be more certain you're giving the car the qualities you want (better launch, better top speed, etc.). And I hope in 6 that the car mastery system gets a major upgrade.

It sucks when your favorite cars have crap boards, and there's not much 'mastery' involved. It'd be cool if we could fill out its skill page, then that unlocked a series of mastery challenges that we could complete to upgrade it's mastery board rarity or something. To unlock another section that then lets weaker cars like the Gremlin get a 7x multiplier. Or maybe then lets us reroll it's page to be focused ob something else like drifting instead of road races. It takes time to port cars to the new games, So I suspect many cars from FH4 will come back through seasonal rewards and updates.

FH4 had far more cars added post launch then any other Forza game, and it would not surprise me if FH5 manages to beat FH4's Post launch car addition count. McLarens are always a safe bet when taking on a competitive street race. In Forza Horizon 5, the McLaren F1GT reigns supreme to its super lightweight body , and 6.1L naturally aspirated V12 engine to boast superior acceleration rates. Able to go zero to 100 mph in 6.9 seconds and reach a top speed of 226 mph, the F1 GT is ideal for both long and short street races. It's even faster than the best JDM cars in GTA 5. The high-performance hypercar boasts a 4.0L twin-turbocharged V8 engine that can crank out 789 horsepower with its 7-speed transmission and rear-wheel-drive train.

Perhaps its most important stats for street racing includes its perfect 10 braking and 9.3 handling scores, which allow the vehicle to maneuver around the most dangerous street obstacles. If you haven't tried this fix, just tweak your graphics card settings in Nvidia or AMD control panel to see if the in-game FPS boosts. Some players fix this issue after modified theire graphics card settings.

So it goes that the user who created that livery has been banned for 8,000 years (yes, that's eight thousand years). The livery has been removed from Forza Horizon 5's online library, although users may still see it on the vehicles of players who already downloaded it. Included in that list are items that feature threats or glorification of physical harm, as is usually the case for any online platform. As a part of the online features, players can create and share custom liveries for their cars. These are essentially just cosmetic skins that players can edit and create.

Forza Horizon 5 players have access to hundreds of cars from various manufacturers to tear up the asphalt across Mexico. The series has always catered to car enthusiasts of every kind and the rise in popularity of electric cars has seen a few appear in-game over the years. For drag racing on automatic transmissions, there's no need to manipulate the clutch at the start. But for high-torque cars, or playing without traction control, you may need to feather the accelerator to get a smooth launch before dropping the hammer. Fast travel in open-world games is pretty typical, but in Forza Horizon 5, it's surprisingly limited.

When you first start playing, you can fast-travel, for free, to a single house that you own, but fast-traveling to any other house or festival hotspot is gonna cost you thousands of credits each time. In most ways, Forza Horizon 5 is an irrefutable success story. However, many players that have experienced Playground Games' latest masterpiece have also encountered a myriad of bugs and issues, many of which detract from FH5's online modes and deter progression. Playground Games has been transparent and communicative about working on these issues, and recently released the Dec. 3, 2021 patch update for Forza Horizon 5 to fix many of these problems.

Its got a nice balance, quite arcadey yet some nice depth with the tuning. I personally prefer this type of game to the more realistic sims. On Dec. 7, we released a fix to tackle the "soft lock" issue which caused Xbox Series X|S players to get stuck with an infinite spinner when saving data. Today's new hotfix goes further and addresses the root cause of the problem. Xbox Series X|S players may have occasionally encountered issues with streaming and soft locks when loading into events, which are now resolved.

There's a sweet spot on cars in the B or A range that aren't too fast but can turn on a dime. Those are the ones you'll want for the majority of you street and road races. You win all those and you'll pretty much unlock whatever else you want to. There's a '68 Ford Mustang fastback I use on a lot on road races. You can max it out on B by focusing on weight reduction and handling and you'll own the competition in street races.

With all that variety, it's no surprise that some players are having loads of fun with the EventLab and creating some of the most unique races seen in any Forza Horizon game. A gamer created a parody car in Forza Horizon 5 featuring KFC and Kim Jong-un which resulted in him being banned from playing Forza Horizon 5 for 8000 years. Of course, the timeline of 8000 years is based on the game but still, it is a long time to wait. A Reddit user, who goes by the name AllThingsRcing in Reddit, shared the story on the social media website stating that his friend got an 8000-year ban for one of his liveries. Swetabh Shekhar is an eSports author at EssentiallySports and holds a Master's degree in Mass Communication.

He has been playing video games since his childhood days and has witnessed the evolution of the gaming industry. GTA, Assassins Creed, Call of Duty, and The Walking Dead are some of his all-time favorites. One gift can be sent per week, along with an additional gift on Christmas Day and New Year's Day. There's another good reason to give -- as player participation grows, the community will unlock the Santa Suit outfit and the 1962 Peel P50 .

That's not a surprise considering howForza Horizonloves to put oddball cars in its games. Progress on these global goals will be tracked in-game. Forza Horizon 5has been out for a little over a month; the game was revealed and got a surprising launch date announcement earlier this year. Featuring a ton of fun multiplayer races, there's plenty to do in the latestForza Horizongame -- and now some new goodies are arriving just in time for the holidays.

But take a moment to at least try the Horizon Arcade early on, which is a rotating set of timed objectives, usually involving destroying something. Horizon Arcade events are marked by a purple blob and a blimp icon on the map. Drive to its location, wait for the event to start, and follow the instructions at the bottom of the screen. Horizon Arcade is a productive way to rack up lots of money, XP, and accolades.

Forza Horizon 5 has lots of display, notification, and controller settings to set the game to your preference, and they're available from the start menu before beginning the game. We recommend the following options in particular, for those playing on a gamepad. Playground Games has been transparent about its efforts to improve Forza Horizon 5, even as we enter the end-of-year holidays. It's important to remain patient as Playground works on resolving the lingering problems in Forza Horizon 5. Many of the fixes in the recent patch update was for several Accolades not actually completing. Most notably, for taking pictures of the statues in the El Camino Horizon Story.

Despite the patch update claiming to have fixed this specific Accolade, it still doesn't complete properly for many players. The accolades are a nice addition for something else to do. Though having ones for creative stuff kinda blows since those will be impossible for most people. Like finish 1000 road races, do Goliath with 100 cars. I don't even understand what this is supposed to mean.

20 years back I've played some racing games, Burnout/NFS HP, i. Mostly those that weren't just straight racing games. But nowadays, I couldn't care less about racing games . I don't care about cars so I didn't care about unlocking new ones. I don't enjoy racing games so I didn't enjoy racing in Forza.

I don't understand why this particular game would change anyone's mind. I'm sure it's a great car racing game but you are still racing cars you know? And if you have no interest as I do this game isn't gonna change your mind imo. The map is one of the most important aspects of the games in the Forza Horizon series and it's no different in Forza Horizon 5. As such, few vehicles in Horizon 5 or even the fastest cars in the Fast and the Furious franchisecan outperform the Divo.

Capable of going 0-60 in 2.8 seconds and in 6.7 seconds, the Mono is the quickest launching street-legal track car in the Forza series. All the latest gaming news, game reviews and trailers The go-to source for comic book and superhero movie fans. To commemorate the occasion, players on Reddit are sharing their final snaps from the game's photo mode. It looks like fans are not happy with the game's current guidelines. One user that goes by the name of "u/Johnny4999" said, "I made a post about this and got eaten alive.

And many fans are confused that how can someone even get access to a car which is yet to be released. According to Reddit poster /u/AllThingsRacing, who claims that the creator of the livery was his friend, the banned player never received any prior warning, nor was he banned prior to this. He also claims that the comically-offensive KFC livery was the creator's very first controversial creation. If those statements are true, then Turn 10 seems quite heavy-handed here indeed. The tales are believable, though, because other players have also complained about first-offense bans, often for much less egregious offenses.

Electric cars are dominating the world in engineering and design and rightfully so. In FH5, players can find some of the most powerful electric and hybrid cars on market. Outside of Forza Horizon 5, there are plenty of supercars and modern sports and track cars that are fueling their power with electric motors.

There's no way to "lose" these races, and you can rewind as far as you want, for any reason. Use these sequences to get a feel for the different cars' handling on different terrain. You want the Bronco to drift and slide without fishtailing, which means you need to be able to finish with a good counter-steer, one that doesn't oversteer, at the end of the slide.